Buenos días.
Cuando el integrando está formado por un producto (o una división, que podemos tratar como un producto) se recomienda utilizar el método de integración por partes que consiste en aplicar la siguiente fórmula:
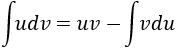
Regla mnemotécnica: Un Día Vi Una Vaca MENOS Flaca Vestida De Uniforme (UDV = UV - FVDU).
Ver demostración de la fórmulaSean y dos funciones, entonces, la derivada del producto es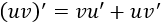
Aplicando integrales en ambos lados de la igualdad (y aplicando la propiedad de la integral de la suma) tenemos:
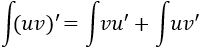
Ahora bien, la integral de la derivada de una función es dicha función, es decir,
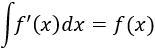
Por tanto,
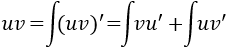
De donde
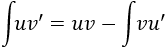
Y ahora sólo tenemos que cambiar la notación: y :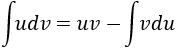
Ejemplo.
A diferencia de las derivadas, no existe una fórmula para poder integrar cualquier producto de funciones. Lo más cercano que tenemos a una regla para integrar producto de funciones es la integración por partes. Curiosamente, se basa en la fórmula para derivar un producto de funciones.
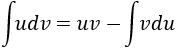
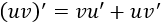
Aplicando integrales en ambos lados de la igualdad (y aplicando la propiedad de la integral de la suma) tenemos:
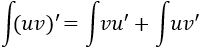
Ahora bien, la integral de la derivada de una función es dicha función, es decir,
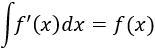
Por tanto,
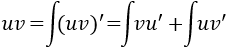
De donde
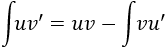
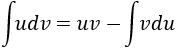
Ejemplo.
Sin embargo, la integración por partes transforma una integral de un producto en otra integral. Esta fórmula no funciona para integrar todos los productos de funciones
La fórmula de la integración por partes es

Observemos que tenemos que derivar  e integrar
e integrar  , por lo que será conveniente que la integral de
, por lo que será conveniente que la integral de  sea sencilla.
sea sencilla.
En general, las funciones polinómicas, logarítmicas y arcotangente se eligen como  . Mientras que las funciones exponenciales, seno y coseno se eligen como
. Mientras que las funciones exponenciales, seno y coseno se eligen como  . Deducción de la fórmula,Supongamos que tenemos las funciones
. Deducción de la fórmula,Supongamos que tenemos las funciones  y
y  . Entonces su derivada está dada por
. Entonces su derivada está dada por

Si integramos ambos lados de la ecuación, obtenemos

Luego, si pasamos  al lado izquierdo, obtenemos
al lado izquierdo, obtenemos

Ejemplo 1. 
Tenemos un producto entre la función 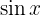 y
y  . Como se mencionó anteriormente, en este tipo de casos se elige
. Como se mencionó anteriormente, en este tipo de casos se elige 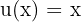 y
y 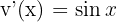 .
.
Derivamos  :
:
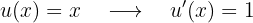
Integramos  :
:
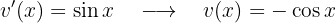
De manera que la integral nos queda
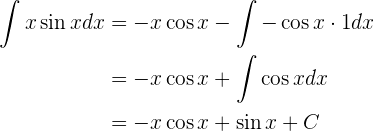
Así,
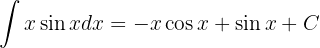
Ejemplo 2.![]()
Tenemos un producto entre la función  y
y  . En este tipo de casos se elige
. En este tipo de casos se elige 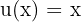 y
y  .
.
Derivamos  :
:
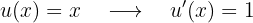
Integramos  :
:

De manera que la integral nos queda
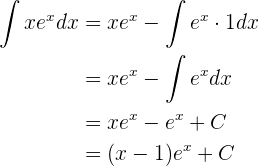
Así,
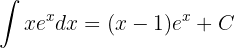




No hay comentarios.:
Publicar un comentario