BUENOS DIAS.
En la clase del sábado pasado nos toco ver el tema de calculo de área entre dos gráficos un tema bastante interesante pero ala ves un poco mas complicado, aun que es un poco mas complicado trato de dar lo mejor de mi y poner mas atención para poder entender mejor así como estudiar mas para aclara mis dudas.
El área entre dos gráficas se calcula mediante la integral definida de la diferencia entre las funciones en el intervalo que abarca las gráficas
El área entre las gráficas de y=f(x) y y=g(x) en el intervalo [a,b] está dada por el valor de la Integral Definida de |f-g| en [a,b].
El área comprendida entre dos funciones es igual al área de la función que está situada por encima menos el área de la función que está situada por debajo.
Él área encerrada por dos funciones 
y 
viene determinada por la siguiente fórmula:
Donde los límites de integración 
y 
corresponden a los puntos de corte entre ambas funciones. Además debe ser mayor o igual que . Que una función sea mayor que otra significa que para el mismo rango de valores de 
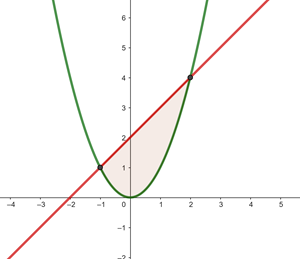
, el valor de la función es mayor y por tanto su gráfica queda representada por encima en los ejes de coordenadas. Ejemplos resueltos del área entre dos funciones1 Calcular el área del recinto limitado por la parábola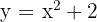 
y la recta que pasa por los puntos 
y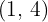 
.
En primer lugar hallamos la ecuación de la recta que pasa por los puntos indicados: Utilizaremos la forma punto-pendiente para encontrar la ecuación de la recta, para esto encontraremos la pendiente con los puntos dados
Utilizando la forma punto-pendiente
Esto lo haremos al resolver la ecuación
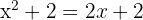
es decir, igualando las funciones
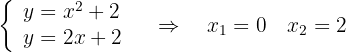
Integrando
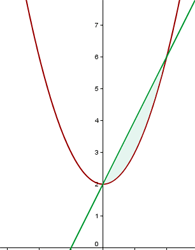
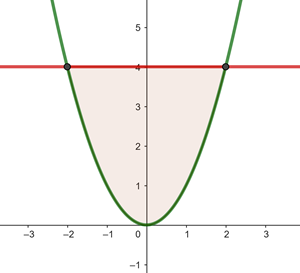
2 Hallar el área de la figura limitada por: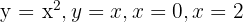 
En primer lugar hallamos los puntos de corte de las dos funciones para conocer los límites de integración:
entonces
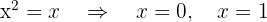
De 
a 
, la recta queda por encima de la parábola
De a 
, la recta queda por debajo de la parábola
entonces
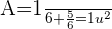
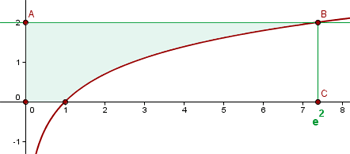
3 Hallar el área de la región del plano limitada por las curvas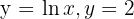 
y los ejes coordenados.
Calculamos el punto de corte de la curva y la recta 
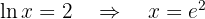
El área es igual al área del rectángulo 
menos el área bajo la curva 
. Tenemos que el área de rectángulo es base por altura, entonces
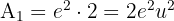
El área bajo la curva es:
entonces
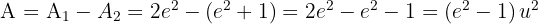
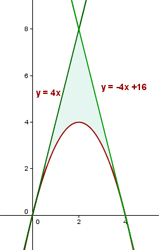
4 Hallar el área del recinto plano y limitado por la parábola 
y las tangentes a la curva en los puntos de intersección con el eje OX.
Puntos de intersección con el eje :
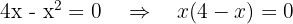
de donde obtenemos que los puntos son 
y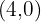 
.
Ecuación de la tangente a la parábola en el punto
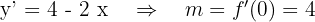
de la forma punto-pendiente de la recta obtenemos que la ecuación es
Ecuación de la tangente a la parábola en el punto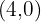
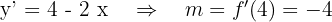
de la forma punto-pendiente de la recta obtenemos que la ecuación es
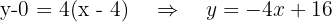
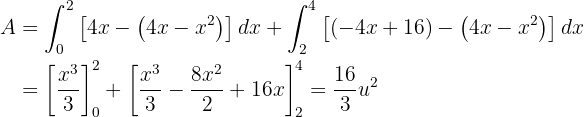
5 Calcular el área limitada por las gráficas de las funciones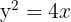 
, 
.
Calculamos los puntos de intersección
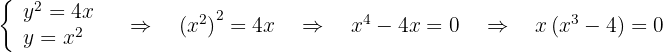
por tanto los puntos de intersección son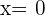 
y 
.
Calcular el área limitada por la parábola 
y la recta 
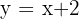
Comenzamos por encontrar los límites de integración igualando las funciones:
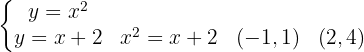
De 
a 
, la recta queda por encima de la parábola.
Entonces el área esta dada por:
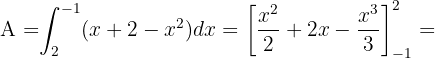
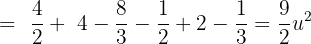
Calcular el área limitada por la parábola y la recta 
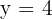
Comenzamos por encontrar los límites de integración igualando las funciones:
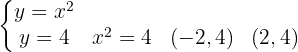
De 
a , la recta queda por encima de la parábola.
Entonces el área esta dada por:
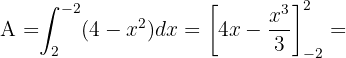
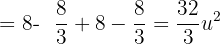
No hay comentarios.:
Publicar un comentario