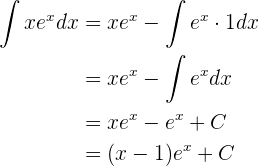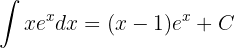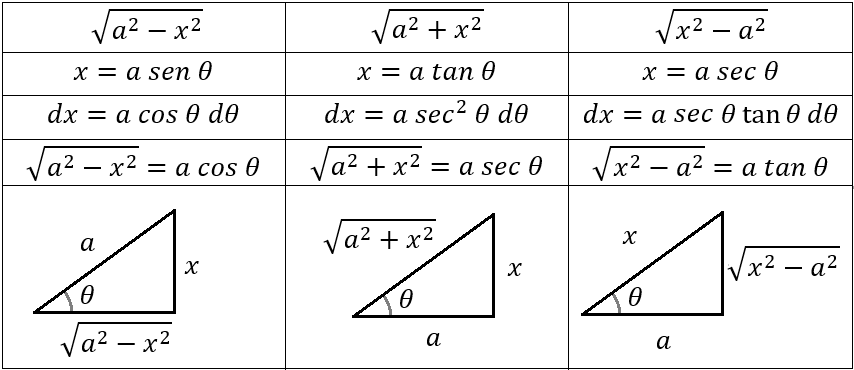buenos días.
El sábado pasado vimos integración por fracciones parciales, Un tema bastante interesante lo cual es nos ayuda con las fracciones mas complejas para realizarlas mas simples de igual manera si es un poco laborioso pero con empeño y practica se que podre entenderle mejor para que no sea tan complicado.
La integración por fracciones parciales es un método de cálculo integral que permite descomponer una fracción compleja en fracciones más simples. Esto facilita el cálculo o la integración de la expresión.
caso 1: factores lineales distintos.
Nota: Todas las integrales que utilicen este caso su resultado sera el logaritmo natural de cada uno de los factores.
caso 2: factores lineales repetidos
caso 3:factores cuadráticos distintos
A todo factor no repetido de segundo grado, como
caso 4: FACTORES CUADRÁTICOS REPETIDOS
A todo factor de segundo grado repetido n veces, como
CASO I
Pasos

abrir like
El cociente de dos polinomios se denomina función racional. La derivación de una función racional conduce a una nueva función racional que puede obtenerse por la regla de la derivada de un cociente. Por otra parte, la integración de una función racional puede conducirnos a funciones que no son racionales.













.png)

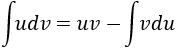

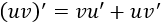
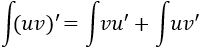
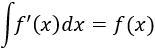
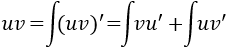
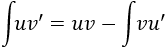










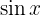

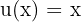
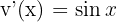
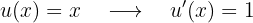

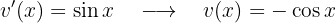
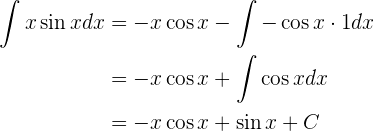
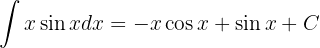
 y
y  .
.