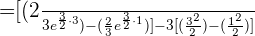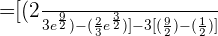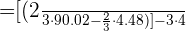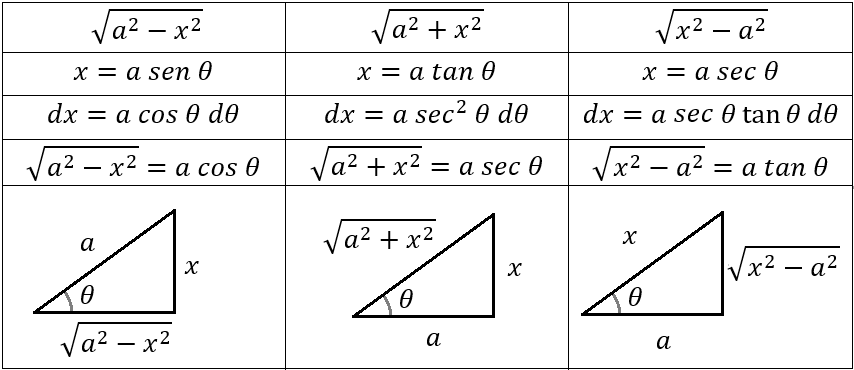La integral definida

 Buenos días. 

En la clase pasada vimos la integral definida, la cual es un tema bastante interesante i la verdad que trato mucho de ponerle mucha atención para entenderle mas por que si seme complica un poco los números pero trato de dar lo mejor de mi.

La integral definida

Desde su origen, la noción de integral ha respondido a la necesidad de mejorar los métodos de medición de áreas subtendidas bajo líneas y superficies curvas. La técnica de integración se desarrolló sobre todo a partir del siglo XVII, paralelamente a los avances que tuvieron lugar en las teorías sobre derivadas y en el cálculo diferencial.

Concepto de integral definida

La integral definida es un concepto utilizado para determinar el valor de las áreas limitadas por curvas y rectas. Dado el intervalo [a, b] en el que, para cada uno de sus puntos x, se define una función f (x) que es mayor o igual que 0 en [a, b], se llama integral definida de la función entre los puntos a y b al área de la porción del plano que está limitada por la función, el eje horizontal OX y las rectas verticales de ecuaciones x = a y x = b.

La integral definida de la función entre los extremos del intervalo [a, b] se denota como:

                             https://www.youtube.com/watch?v=K15rvmw2WwI

Propiedades de la integral definida

La integral definida cumple las siguientes propiedades:

• Toda integral extendida a un intervalo de un solo punto, [a, a], es igual a cero.
• Cuando la función f (x) es mayor que cero, su integral es positiva; si la función es menor que cero, su integral es negativa.
• La integral de una suma de funciones es igual a la suma de sus integrales tomadas por separado.
• La integral del producto de una constante por una función es igual a la constante por la integral de la función (es decir, se puede «sacar» la constante de la integral).
• Al permutar los límites de una integral, ésta cambia de signo.
• Dados tres puntos tales que a < b < c, entonces se cumple que (integración a trozos):
  

• Para todo punto x del intervalo [a,b] al que se aplican dos funciones f (x) y g (x) tales que f (x) £ g (x), se verifica que:
  

Ilustración gráfica del concepto de integral definida.

Función integral

Considerando una función f continua en [a, b] y un valor x Î [a, b], es posible definir una función matemática de la forma:

donde, para no inducir a confusión, se ha modificado la notación de la variable independiente de x a t. Esta función, simbolizada habitualmente por F (x), recibe el nombre de función integral o, también, función área pues cuando f es mayor o igual que cero en [a, b], F (x) nos da el área.

Interpretación geométrica de la función integral o función área.

Teorema fundamental del cálculo integral

La relación entre derivada e integral definida queda establecida definitivamente por medio del denominado teorema fundamental del cálculo integral, que establece que, dada una función f (x), su función integral asociada F (x) cumple necesariamente que:

A partir del teorema fundamental del cálculo integral es posible definir un método para calcular la integral definida de una función f (x) en un intervalo [a, b], denominado regla de Barrow:

• Se busca primero una función F (x) que verifique que F¿ (x) = f (x).
• Se calcula el valor de esta función en los extremos del intervalo: F (a) y F (b).
• El valor de la integral definida entre estos dos puntos vendrá entonces dado por:


Abrir li ke

Definición de la integral definida  Dada una función f(x) de una variable real x y un intervalo [a,b] de la recta real, la integral definida es igual al área limitada entre la gráfica de f(x), el eje de abscisas, y las líneas verticales x = a y x = b.

Se representa por  .

•   es el signo de integración.
• a es el límite inferior de la integración.
• b es el límite superior de la integración.
•  es el integrando o función a integrar.
•  es el diferencial de x  y nos indica cuál es la variable de la función que se integra.
• Propiedades de la integral definida

1 El valor de la integral definida cambia de signo si se permutan los límites de integración.

Esta propiedad nos puede servir para no operar con signos negativos.

Ejemplo: 

2 Si los límites de integración coinciden, la integral definida vale cero.

En realidad, al tener el mismo límite de integración en ambos extremos no existe ningún área a calcular, es por eso que la integral es igual a cero en este caso.

ejemplo.   

3 Si c es un punto interior del intervalo [a, b], la integral definida se puede descomponer como una suma de dos integrales extendidas a los intervalos [a, c] y [c, b].

Al estar el punto c entre a  y b sobre el eje de las abcisas, el  área limitada por el intervalo [a,b] es la suma de las áreas limitadas por [a,c] y [c,d], lo mismo ocurre con el valor de la integral.

Ejemplo. Para 7 que pertenece al intervalo [3,10]

4 La integral definida de una suma de funciones es igual a la suma de integrales.

Esta propiedad nos puede servir para no tener expresiones muy largas dentro de una misma integral y así manipular y hacer cálculos más facilmente , o en el otro caso,  agrupar  expresiones para un cálculo más cómodo.

Ejemplo: Para  y  ,

5   La integral del producto de una constante k por una función es igual a la constante k multiplicada por la integral de la función.

Esto es sacar la constante fuera de la integral.

Ejemplo: Para la constante k=3

 Ejemplo de aplicación

En éste ejemplo implementaremos las propiedades anteriores en una aplicación de la integral en crecimiento poblacional, para una mejor visualización.

Una población crece con una tasa de 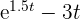 individuos por año (donde  es el número de años).  En el primer año la población es de 1500 personas.

¿Cuánto creció la población  entre en primer y tercer año?, ¿Cuál es la población en el tercer año?

1  Dado que nos pide el crecimiento de la población entre 1 y 3, es decir, el área bajo la curva de la tasa de crecimiento entre 1 y 3, lo expresaremos como sigue:

Nota: los pasos siguientes son para ilustrar el uso de las propiedades, algunos de ellos pueden ser omitidos.

2 Al hacer los cálculos,  notemos que podemos usar la propiedad 4 y separamos en una suma.

3  También podemos utilizar la propiedad 5 y sacamos el la constante -3 que multiplica a t.

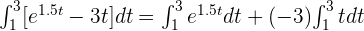
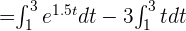
4 Dado que 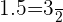 sustituimos y hacemos los cálculos que correspondientes para hallar la respuesta a la primera pregunta:

La integral indefinida

 Buenos días.

En la clase pasada vimos la integral indefinida es un tema bastante interesante, pero no voy anegar que seme ase un poco complicado agárrale el ritmo delos problemas mas que nada  cuando nos tocan ejercicios con rais a mi en lo personal llega mucho a confundirme  en el aspecto de como sacar los números decimales.

¿Qué es una integral indefinida?

Una integral indefinida es una operación matemática que consiste en calcular la función primitiva de una función. Es decir, dada una función f(x), la integral indefinida de la función f(x) es igual al conjunto de funciones que al ser derivadas dan como resultado f(x).

Así pues, la función obtenida de resolver una integral indefinida se llama función primitiva.

•  es el signo de integración.
•  es la función a integrar.
•  es el diferencial de x, que indica la variable de la función que se integra.
•  es la función resultado de la integral.
• Integral de una constante:

  

• Integral de una potencia:

  

• Integrales de funciones exponenciales:

  

  

• Integrales logarítmicas:

  

  

  

• Integrales trigonométricas:

  

  

  

• Métodos de integración y de las propiedades de las integrales.

  

Linealidad de la integral indefinida

.

La primitiva es lineal, es decir:

1. Si f es una función que admite una primitiva F sobre un intervalo I, entonces para todo real k, una primitiva de kf sobre el intervalo I es kF.
2. Si F y G son primitivas respectivas de dos funciones f y g, entonces una primitiva de f + g es F + G.

La linealidad se puede expresar como sigue:

${\displaystyle \int (k\cdot f\left(x\right)+l\cdot g\left(x\right))=k\cdot \int f\left(x\right)+l\cdot \int g\left(x\right)}$

En cálculo infinitesimal, la función primitiva o antiderivada de una función f es una función F cuya derivada es f, es decir, F ′ = f.

Una condición suficiente para que una función f admita primitivas sobre un intervalo es que sea continua en dicho intervalo.

Si una función f admite una primitiva sobre un intervalo, admite una infinidad, que difieren entre sí en una constante: si F₁ y F₂ son dos primitivas de f, entonces existe un número real C, tal que F₁ = F₂ + C. A C se le conoce como o ¿constante de integración  Como consecuencia, si F es una primitiva de una función f, el conjunto de sus primitivas es F + C. A dicho conjunto se le llama integral indefinida de f y se representa como:

${\displaystyle \int f}$   o bien   ${\displaystyle \int f(x)dx}$

El campo vectorial definido asigna un vector (1,f(x)) a cada punto  del plano donde . Se muestran tres curvas de las infinitas posibles curvas primitivas de  que se pueden obtener variando la constante de integración.

Ejemplo

Una primitiva de la función ${\displaystyle f(x)=\cos (x)}$ en ${\displaystyle \mathbb{R},}$ es la función ${\displaystyle F(x)=\sin (x)}$ ya que:

${\displaystyle \frac{d}{dx}(\sin (x))=\cos (x)\mathrm{\forall }x\in \mathbb{R}}$

Dado que la derivada de una constante es cero, tendremos que cos(x) tendrá un número infinito de primitivas tales como sin(x), sin(x) + 5, sin(x) - 100, etc. Es más, cualquier primitiva de la función f(x) = cos(x) será de la forma sin(x) + C donde C es una constante conocida como constante de integración.

La constante de integración.

La derivada de cualquier función constante es cero. Una vez que se ha encontrado una primitiva F, si se le suma o resta una constante C, se obtiene otra primitiva. Esto ocurre porque (F + C) ' = F ' + C ' = F ' + 0 = F '. La constante es una manera de expresar que cada función tiene un número infinito de primitivas diferentes.

Abril Like.