ola buenos días.
Bueno lo que vi en la clase del sábado pasado fue la determinación de máximo y mínimo de una función, aun que llegue un poco tarde ese día no pude verlo como tal pero con lo videos me guio y trato siempre de aprovechar al máximo para retener la mayor información posible.
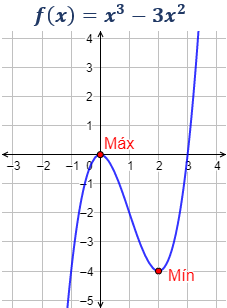
La determinación del máximo y mínimo de una función es una de las aplicaciones de la derivadas con mayor importancia, veamos en qué consiste:
Se entiende por máximo o mínimo al valor mas grande o valor mas pequeño que puede adquirir una función en un punto de su gráfica.
Imagina una montaña y un valle. El punto más alto de la montaña sería un máximo, mientras que el punto más bajo del valle sería un mínimo. De manera similar, en una función matemática, el máximo es el valor más alto que puede alcanzar la función en un intervalo, y el mínimo es el valor más bajo.
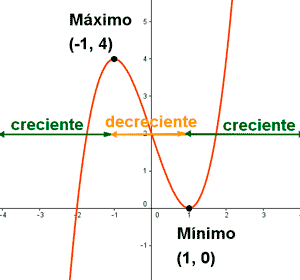
Existen dos tipos de máximos y mínimos: absolutos y relativos. Los máximos y mínimos absolutos son los puntos más altos y más bajos en todo el dominio de la función. Por otro lado, los máximos y mínimos relativos son los puntos más altos y más bajos en una región específica del dominio de la función.

En la gráfica anterior, los puntos P1, P2, P3, Q1, Q2 y Q3 representan los puntos críticos de cada función y al mismo tiempo según el caso:
- P1 es el punto máximo absoluto de la primera función
- P2 es un mínimo relativo
- P3 es un máximo relativo
- Q1 es un mínimo relativo
- Q2 es un máximo relativo
- Q3 es un mínimo absoluto de la segunda función
ejemplos:
El máximo absoluto de una función ![]() en un intervalo cerrado
en un intervalo cerrado ![]() es el mayor valor que toma la función en todo el intervalo.
es el mayor valor que toma la función en todo el intervalo.
El mínimo absoluto de una función ![]() en un intervalo cerrado
en un intervalo cerrado ![]() es el menor valor que toma la función en todo el intervalo.
es el menor valor que toma la función en todo el intervalo.
Si nos planteamos el problema de hallar el máximo y el mínimo absolutos de una función ![]() en un intervalo cerrado
en un intervalo cerrado ![]() , habremos de considerar tres clases de puntos:
, habremos de considerar tres clases de puntos:
a) los puntos críticos o singulares de f en ![]() .
.
b) Los extremos a y b.
c) Los puntos de ![]() en los que f no es derivable.
en los que f no es derivable.
Si x es un punto máximo o mínimo absoluto de f sobre ![]() , entonces x será un punto de una de las tres clases arriba citadas.
, entonces x será un punto de una de las tres clases arriba citadas.
El procedimiento para calcular el máximo y el mínimo de una función f en un intervalo cerrado ![]() es bastante sencillo:
es bastante sencillo:
a) Primero se calcula ![]() para todos aquellos puntos x para los cuales
para todos aquellos puntos x para los cuales ![]() , es decir el valor de la función en los puntos críticos.
, es decir el valor de la función en los puntos críticos.
b) Después se calcula ![]() en los puntos x en los que f no es derivable.
en los puntos x en los que f no es derivable.
c) Finalmente se calculan ![]() y
y ![]()
El mayor de todos estos valores será el máximo absoluto, y el menor de todos ellos será el mínimo absoluto.
Ejemplo:
a) Calcular el máximo y el mínimo absolutos de la función
![]() en el intervalo
en el intervalo ![]() .
.
En primer lugar derivaremos la función: ![]()
Luego igualamos esa primera derivada a cero: ![]()
y resolvemos la ecuación así obtenida. En este caso ![]()
El valor ![]() está en el intervalo
está en el intervalo ![]() , luego el primer conjunto de “candidatos” a máximos o mínimos es
, luego el primer conjunto de “candidatos” a máximos o mínimos es ![]()
El segundo conjunto contiene a los extremos del intervalo: ![]()
El tercer conjunto (el conjunto de los puntos donde la función no es derivable) no tiene ningún valor en este caso, pues la función es derivable en todos los puntos del intervalo (es un polinomio y sabemos que todos los polinomios son derivables en cualquier punto de su dominio hasta el orden que deseemos).
Por último, sólo tenemos que calcular los valores que toma la función en esos puntos:

Por lo tanto el mínimo absoluto es ![]() , en el punto
, en el punto ![]() , y el máximo absoluto es 20, en el punto
, y el máximo absoluto es 20, en el punto ![]() .
.
Ejemplo