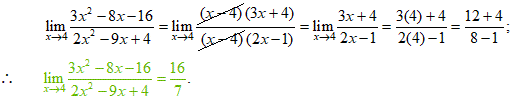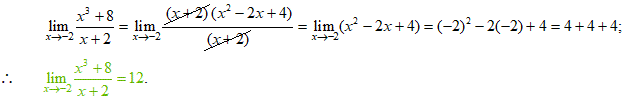Limite por Factorización y Racionalización

Aprendiendo:

Segunda clase:

Bueno tuve una semana un poco casado por el trabajo pero a andamos con toda la actitud para ir aprendiendo un poquito mas acerca de la factorización y racionalización así mismo aprovechar al máximo la clase para ir obteniendo un poco mas de conocimiento en calculo.  

La factorización y la racionalización

• Factorización: Para evaluar el límite de una función racional en un agujero, se puede factorizar el numerador y el denominador, cancelar los factores y luego evaluar el límite por sustitución directa. 
• Racionalización: Para racionalizar una fracción, se multiplica el numerador y el denominador por un factor que elimine las raíces, ya sean del numerador o del denominador. La nueva expresión debe ser equivalente original. 
• 
  
• Para evitar indeterminaciones en los límites, se puede reducir el cociente a otro cuyo denominador no sea cero. Esto se puede hacer factorizando el numerador y/o el denominador, y luego cancelando los factores comunes. 

Ejemplos:

     

 

• Para estos limites tenemos que tener en cuenta lo siguiente: Conjugado de un termino

Es un binomio que se toma con diferente signo entre dos factores.

Ejemplo:

• Para resolver los limites se realiza los siguientes pasos:

1. Se escribe el conjugado del termino que tenga raíz
2. Se multiplica el numerador y el denominador por el conjugado
3. Se realiza las operaciones de multiplicación
4. Se elimina el termino que se resuelve cero en el denominador y en el caso de ser necesario se factoriza
5. Se evalúa el valor del limite                  

Link para descargar

Teorema de límites

 Primera clase:

Mi forma de aprendizaje es escribir i ir visualizando, por lo que me gusta ver videos para poder aprender mas, sobre todo ir practicando por que la materia será todo un reto para mi pero así mismo mis ganas de superarme siempre irán con migo. además siempre me causa curiosidad aprender aun mas i poner como prioridad todas mis metas.

 Nada mejor que ir aprendiendo poco apoco alado de  una persona que su objetivó es enseñar dejarnos sabiduría acerca de esta materia.

Los grandes creadores del Cálculo diferencial fueron el inglés Isaac Newton (1642–1727) y el alemán Gottfried Wilhelm Leibniz (1646–1716). De manera diferente pero independientemente estos grandes intelectuales de los siglos XVII y XVIII sistematizaron y generalizaron ideas y procedimientos que habían sido abordados (de diferentes maneras) y con éxito parcial desde la Antigüedad. Antes de Newton y Leibniz fueron realizados diversos aportes de importancia asociados al nombre de grandes personalidades como por ejemplo: Gilles de Roberval, Johannes Kepler, René Descartes, Pierre de Fermat, Galileo Galilei.

 

https://www.blogger.com/blog/post/edit/6500354309258209537/7967487444762448125

Si es posible aplicar directamente las propiedades anteriores, el límite se calcula directamente. Con respecto a las propiedades, como la propiedad 6 se aplica a cualquier polinomio y las propiedades 1, 2, 3, y 4  implican funciones polinómicas es indistinto que nos refiramos a cada una de las propiedades 1 a 4 en particular que a la propiedad 6 cuando calculamos el límite de una función polinómica. Lo mismo, la propiedad 7 se aplica a una función racional y la propiedad 4 (III) también.      Cuando al sustituir la a por x en la función nos da la forma indeterminada 0/0 es posible calcular el límite pero, previamente, hay que transformar la fórmula de la función de tal modo que, una vez hecha la simplificación pertinente, se pueda evitar la división por cero: para lograr esto disponemos de procedimientos algebraicos eficaces como la factorización, la conjugada, etc.

Ejercicios resueltos           Evalué los siguientes límites indicando la propiedad o propiedades que se aplican en cada paso:

S o l u c i o n e s

 1. Solución

 2. Solución:

 3. Solución:

 4. Solución:

 5. Solución:

 6. Solución:

No es posible aplicar directamente el TL7, pues se obtendría la forma indeterminada 0/0; no obstante, luego de factorizar y simplificar la expresión, se obtiene fácilmente el límite aplicando el TL1:

 7. Solución:

No es posible aplicar directamente el TL7, pues se obtendría la forma indeterminada 0/0; no obstante, luego de factorizar y simplificar la expresión se obtiene fácilmente el límite aplicando el TL7 o el TL4(III):

 8. Solución:

Si pretendiéramos aplicar el límite directamente a partir del TL7, nos daría la forma indeterminada 0/0;

por lo que, se debe factorizar y luego simplificar la expresión antes de poder hacer uso del TL6:

 9. Solución:

No se puede aplicar el límite directamente, daría la forma indeterminada 0/0; no obstante, luego de multiplicar tanto el numerador como el denominador por la conjugada de la expresión en el numerador y luego reduciendo y simplificando, se puede aplicar el TL para hallar el límite:

 10. Solución:

Luego de la transformación de la expresión se aplican los TL7  y  TL8:

 11. Solución:

El límite no se puede aplicar directamente, resultaría la forma indeterminada 0/0; no obstante, una vez factorizando y simplificando, la expresión queda expedita para hallar el límite mediante los TL7  y  TL6:

 12. Solución: