Buenos días 

En la clase del sábado vimos el tema de la sustitución trigonométrica el tema bastante interesante aun que tengo que admitir que seme izo un poco complicado pero con practica y viendo videos se que podre entenderle mucho mas y así mismo poder obtener mas aprendizaje.

Sustitución Trigonométrica

La sustitución trigonométrica es un método de integración. En lugar de sustituir usando una nueva variable que es función de x (u=f(x)), se define a x como una función trigonométrica de una nueva variable (x=f(θ)).

El método consiste en:

• Reescribir la ecuación en términos de la variable (θ) y su diferencial (dθ)
• Resolver la integral
• Reescribir el resultado en términos de x

Sirve para los siguientes casos:

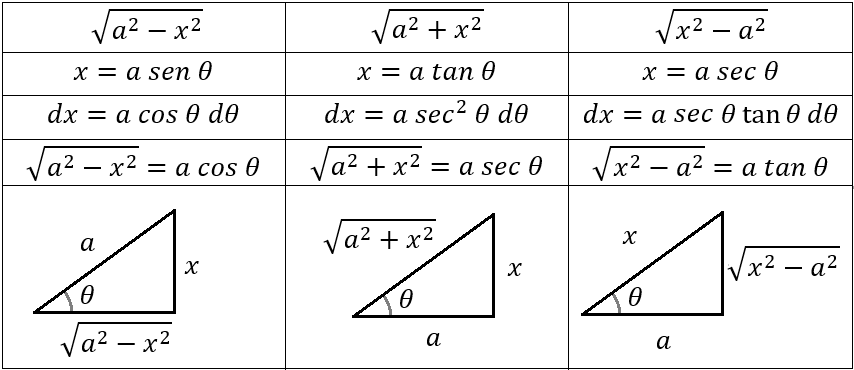
En la tabla se muestra como se deben sustituir la variable x y el diferencial dx.

Después de realizar la integración es recomendable dibujar un triangulo rectángulo en donde se relacionen x, a y  θ para regresar la función a términos de x.

Ejemplo:

Hallar la siguiente integral usando el método de sustitución trigonométrica:

A) y= √(a2-x2) / x2

x= a sen θ      dx= a cos θ dθ

Abrir like

Integrales que implican a2−x2−−−−−−√$\sqrt{a^2-x^2}$

Antes de desarrollar una estrategia general para las integrales que contienen a2−x2−−−−−−√,$\sqrt{a^2-x^2},$ considere la integral ∫9−x2−−−−−√dx.${\displaystyle \int \sqrt{9-x^2}}dx.$ Esta integral no puede evaluarse con ninguna de las técnicas sobre las que hemos hablado hasta ahora. Sin embargo, si hacemos la sustitución x=3senθ,$x=3\text{sen}\theta ,$ tenemos dx=3cosθdθ.$dx=3\text{cos}\theta d\theta .$ Después de sustituir en la integral, tenemos

∫9−x2−−−−−√dx=∫​9−(3senθ)2−−−−−−−−−−√3cosθdθ.$${\displaystyle \int \sqrt{9-x^2}dx}={{\displaystyle \int }}^{\text{}}\sqrt{9-{(3\text{sen}\theta )}^2}3\text{cos}\theta d\theta .$$

Tras simplificar, tenemos

∫​9−x2−−−−−√dx=∫​91−sen2θ−−−−−−−−√cosθdθ.$${{\displaystyle \int }}^{\text{}}\sqrt{9-x^2}dx={{\displaystyle \int }}^{\text{}}9\sqrt{1-{\text{sen}}^2\theta }\text{cos}\theta d\theta .$$

Supongamos que 1−sen2θ=cos2θ,$1-{\text{sen}}^2\theta ={\text{cos}}^2\theta ,$ ahora tenemos

∫​9−x2−−−−−√dx=∫​9cos2θ−−−−√cosθdθ.$${{\displaystyle \int }}^{\text{}}\sqrt{9-x^2}dx={{\displaystyle \int }}^{\text{}}9\sqrt{{\text{cos}}^2\theta }\text{cos}\theta d\theta .$$

Suponiendo que cosθ≥0,$\text{cos}\theta \ge 0,$ tenemos

∫​9−x2−−−−−√dx=∫​9cos2θdθ.$${{\displaystyle \int }}^{\text{}}\sqrt{9-x^2}dx={{\displaystyle \int }}^{\text{}}9{\text{cos}}^2\theta d\theta .$$

En este punto, podemos evaluar la integral utilizando las técnicas desarrolladas para integrar potencias y productos de funciones trigonométricas.